Homework 1

info

Q1 Loop-carried dependences For this question, we will describe a loop-carried dependence as coming from some statement in iteration (i,j) to some other iteration (x,y), where x and y are written as expressions involving i and j (e.g., (i,j+1)). For example, there could be a loop-carried dependence from S4(i,j) to S5(i+1,j). Note that the first statement must come before the second statement in program order. Consider the code below, where all variables have been previously declared.

...
for (i=1; i <= N; i++) {
  for (j=1; j <= i; j++) {
    S1: a[i][j] = b[i][j] + c[i][j];
    S2: b[i][j] = a[i-1][j-1] * b[i+1][j-1] * c[i-1][j];
    S3: c[i+1][j] = a[i][j];
  }
}
...

Thinking

• Finding dependencies inside iteration:
  • $S_{1} \mathop{\to}^T S_{3}$
  • $S_{1} \mathop{\to}^{A} S_{2}$
• Finding dependencies across iterations
  • $S_{1}[i,j]\mathop{\to}^T S_{2}[i+1,j+1]$
  • $S_{2}[i,j]\mathop{\to}^A S_{2}[i+1,j-1]$
  • $S_{3}[i,j]\mathop{\to}^T S_{1}[i+1,j]$
  • $S_{3}[i-1,j]\mathop{\to}^T S_{2}[i+1,j]$, normalized to $S_{3}[i,j]\mathop{\to}^T S_{2}[i+2,j]$

info

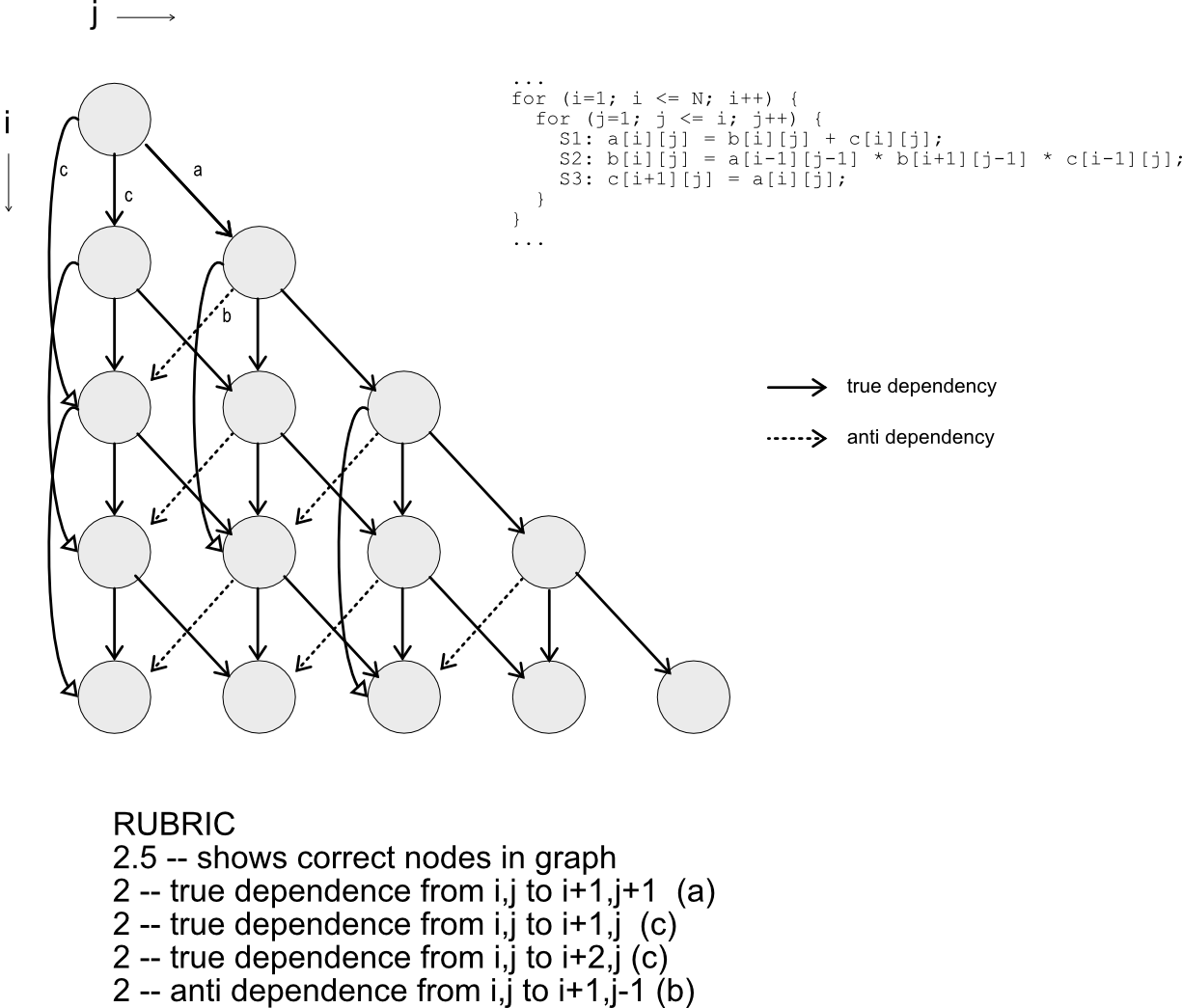
Q1.1 LDG Draw LDG for this loop nest

LDG does not reflect loop-independent dependency, each node in LDG represents all statements in a particular iteration. Therefore, only dependencies across iterations should be included:

Figure: LDG of Q1

danger

Notice that the loop variable j <= i, therefore, there are no data dependences below the diagonal of the graph.

[!success] Answer from TA

info

Q2 Variable scope analysis Consider the code below. All matrices have dimension $N\times N$, all vectors have dimension $N$, and assume that $N$ is divisible by $2$.

...
for (i=0; i<N; i++) {
  k = C[N-1-i];
  for (j=0; j<N; j++) {
    A[i][j] = k * A[i][j] * B[i/2][j];
  }
}
...

info

Q2.1 $i$-loop By default, all variables are shared. If the $i$-loop is converted to a parallel loop, indicate which variables should be private.

Thinking: Applying parallelism on $i$ loop, $i$ should be private to each thread, and things related to $i$ should be private too.

• $i$: each thread should have its own $i$. Make $i$ private.
• $j$: its originally private if $i$ loop is parallel
• $k$: its assigned within $i$ loop but not $j$ loop. Make $k$ private.\
• $A$: its being read and written, but since the access index $i,j$ is private, then access to $A$ is thread safe. So $A$ can be shared.
• $B$: its read only, can be shared.
• $C$: its read only, can be shared. Therefore, $i$, $j$, $k$ are private.

info

Q2.2 $j$-loop By default, all variables are shared. If the $j$-loop is converted to a parallel loop, indicate which variables should be private.

Thinking: Applying parallelism on $j$ loop, $j$ should be private to each thread, and things related to $j$ should be private.

• $i$: it has the same value and its read only for $j$ loops inside the same $i$ loop iteration, can be shared.
• $j$: each thread should have its own $j$. Make $j$ private.
• $k$: same as $i$, can be shared.
• $A$: The same as $i$ loop parallelism, no race condition between different $j$.
• $B$: its read only, can be shared.
• $C$: its read only, can be shared. Therefore, $j$ is private.

info

Q3 Average access latency Suppose you have a one-level (L1) cache. The L1 latency is 2 cycles, and memory latency is 80 cycles.

info

Q3.1 Calculate AAT If the L1 miss rate is 0.05, what is the average latency for a memory operation?

$$AAT = T_{L_{1}} + M_{L_{1}}\cdot T_{Mem} = 2+0.05\times 80 = 6 (cycles)$$

info

Q3.2 Calculate miss rate What must the miss rate be in order to achieve an average access latency of 10 cycles?

$$\begin{align} AAT = T_{L_{1}} + M_{L_{1}}\cdot T_{Mem} = 2+M_{L_{1}}\cdot 80 = 10 \\ M_{L_{1}} = \frac{10-2}{80} = 0.1 \end{align}$$

info

Q4 Average access latency (two-level) Suppose you have a two-level cache. The L1 access latency is 2 cycles. The L2 access latency is 10 cycles. The memory access latency is 80 cycles.

info

Q4.1 Calculate AAT If the L1 miss rate is 0.1, and the L2 miss rate is 0.5, what is the average access latency?

$$\begin{align} ATT &= T_{L_{1}} + M_{L_{1}} \cdot T_{L_{2}} + M_{L_{1}}\cdot M_{L_{2}} \cdot T_{Mem} \\ &=2+0.1\times 10 + 0.1\times 0.5 \times 80 \\ &=7(cycles) \end{align}$$

info

Q4.2 Calculate L2 miss rate If the L1 miss rate is 0.05, what must the L2 miss rate be to achieve an average access latency of 4 cycles?

$$\begin{align} ATT &= T_{L_{1}} + M_{L_{1}} \cdot T_{L_{2}} + M_{L_{1}}\cdot M_{L_{2}} \cdot T_{Mem} &=4\\ &=2+0.05\times 10 + 0.05\times M_{L_{2}} \times 80 &=4 \\ M_{L_{2}}&=\frac{4-2-0.05\times 10}{80\times 0.05}=0.375 \end{align}$$

info

Q5 Replacement policy You have a fully-associative cache with a capacity of four blocks. Blocks are stored in positions 0, 1, 2, 3 in the set, from left to right in the figure. To write the content of the cache, list the block addresses in left-to-right order, and use a single hypen (-) to denote a block position that does not contain a valid block. Empty blocks are filled from left to right. As shown, the initial cache state is A,-,-,-.

The cache uses LRU replacement and has a write-no-allocate policy. After each memory operation below, show the state of the cache. Access sequence: Read B, Write A, Read C, Write D, Read C, Read E, Read D, Write C, Read B, Read F

It has a write no allocate policy, therefore write miss will not cause the block to be loaded into cache, only read miss will.