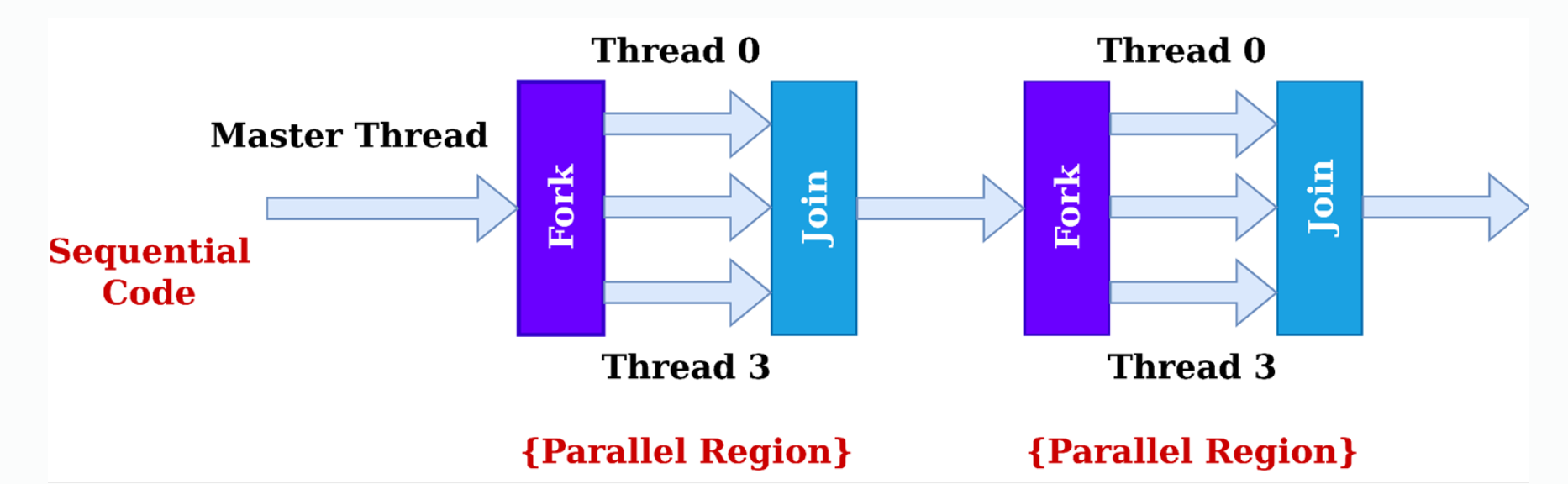
Data Dependency

Data Dependences

concurrent != parallel control parallel != data parallel

speed up limitations:

• dependencies
• communication overheads
• synchronization

dependencies that prevent parallel execution:

• resource dependency: wash multiple clothes with single watching machine measure parallelism: Flynn's Taxonomy

info

Definition: Data Dependency Assuming statement $S_{1}$ and $S_{2}$, $S_{2}$ depends on $S_{1}$ if:

$$[I(S_{1})\cap O(S_{2})] \cup [O(S_{1}) \cap I(S_{2})] \cup [O(S_{1})\cap O(S_{2})] = \emptyset$$

where

• $I(S_{i})$ is the set of memory locations read by $S_{1}$
• $O(S_{j})$ is the set of memory locations written by $S_{j}$

Three cases exist:

• Anti-dependency (Write After Read): $I(S_{1}) \cap O(S_{2}) \neq \emptyset, S_{1}\to S_{2}$ and $S_{1}$ reads before $S_{2}$ overwrites it. Written as $S_{1}\rightarrow A\ S_{2}$.
• True dependency (Read After Write): $O(S_{1}) \cap I(S_{2}) \neq \emptyset, S_{1} \to S_{2}$ and $S_{1}$ writes before something read by $S_{2}$. Written as $S_{1} \to T\ S_{2}$
• Output dependency (Write After Write): $O(S_{1}) \cap O(S_{2}) \neq \emptyset, S_{1} to S_{2}$ and both write to the same memory location. Written as $S_{1} \rightarrow O\ S_{2}$

note

There will be no concurrency problems for read after read, only with write the problem is to be addressed.

note

Example: True Dependency

note

Example: Anti Dependency

note

Example: Output Dependency

tip

True dependence is the case that we most worry about.

note

• For anti-dependence

$$\begin{align} S_{1}[i,j] \rightarrow A\ S_{1}[i+1,j] \\ S_{1}[i,j] \rightarrow A\ S_{1}[1,j+1] \end{align}$$

• For true dependence:

$$\begin{align} S_{1}[i,j] \rightarrow T\ S_{1}[i,j+1] \\ S_{1}[i,j] \rightarrow T\ S_{1}[i+1,j] \end{align}$$

• For output dependence: None

Loop-carried Dependences

info

What is Iteration-space Traversal Graph (ITG)? The ITG shows graphically the order of traversal in the iteration space. This is sometimes called the happens-before relationship. In an ITG:

• A node represents a point in the iteration space
• A directed edge indicates the next-point that will be encountered after the current point is traversed

note

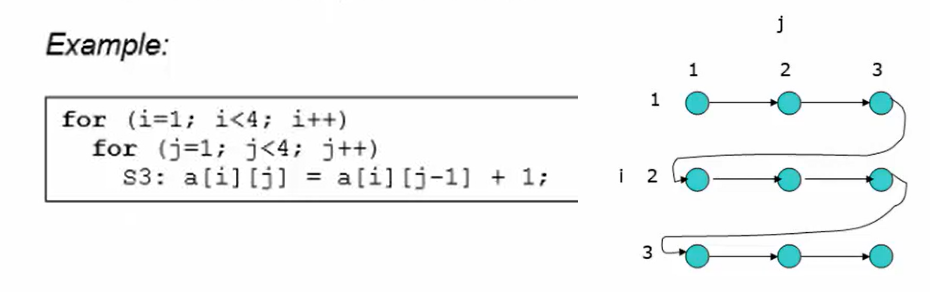In example above:

• It is loop-carried on for j loop
• There is no loop-carried dependence in for i loop

note

• For anti-dependence:

$$\begin{align} S_{2}[i,j] \rightarrow A\ S_{3}[i,j] \end{align}$$

• For true dependence:

$$\begin{align} S_{2}[i,j] \rightarrow S_{3}[i,j+1] \end{align}$$

• For output dependence: None

Draw the LDG:

tip

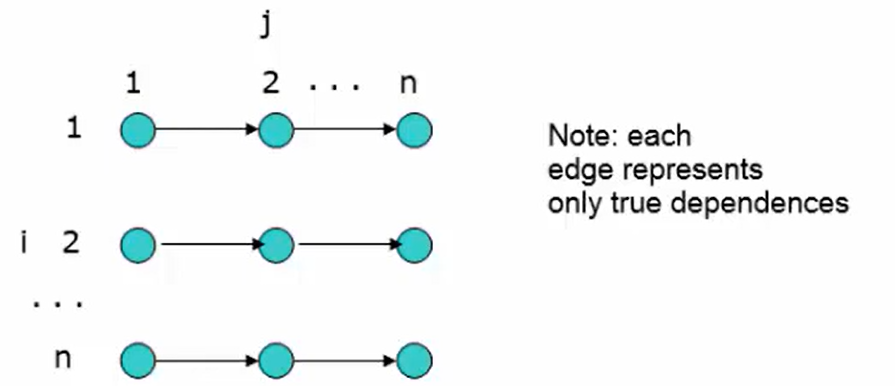
LDG is useful because it shows how can you parallel the code, for the above example, applying parallelism along $i$ axis(modifying $j$ only in each thread) is possible according to the LDG.

[!TIP] Why is the anti-dependence not shown on the graph? LDG does not show loop-independent dependences, because a node represents all statements in a particular iteration,

warning

Identifying things that can be written in parallel code with LDG is machine independent, which means that we do not care about memory access patterns, and machine dependent factors.

OpenMP

#pragma omp parallel for
for(int i=1; i<n; i++)
	for(int j=1; j<N, j++)
		a[i][j] = a[i][j-1] + 1;