Amhdal's Law

Speedup of Parallel Execution

info

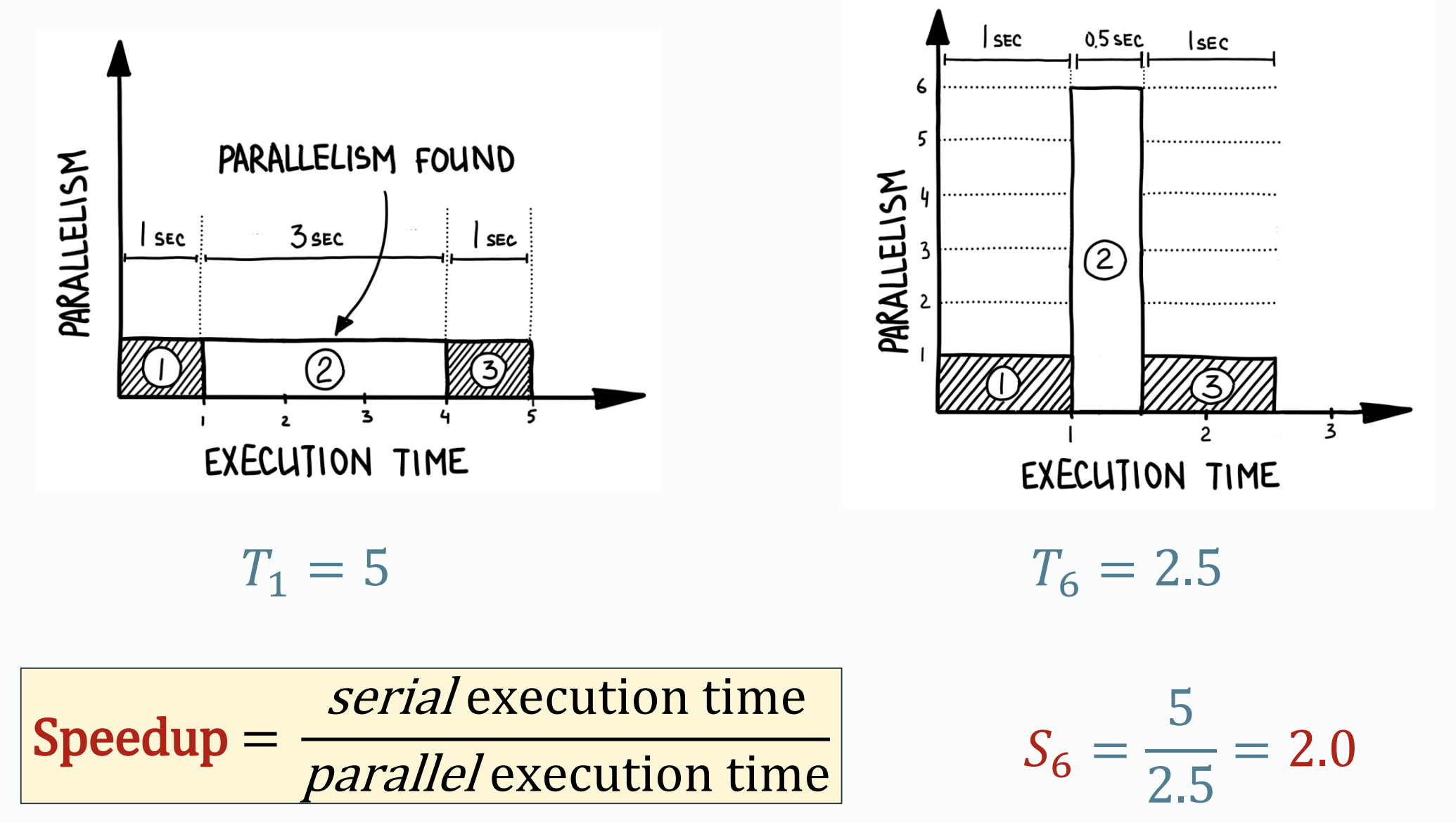
Definition: Speed up Speed up is defined as:

$$\frac{time\ of\ serial\ execution}{time\ of\ parallel\ execution}$$

Note that the time of serial execution should be the time for serial execution of best serial algorithm because bad programs often have good speedup.

Suppose that a program is composed of a serial phase and a parallel phase, the whole program runs for $1$ time unit, the serial phase runs for time $s$, and the parallel phase for time $1-s$.

Amdahl's Law

note

Amdahl's law Regardless how many processors $N$ are used, the execution time of the program will be at least $s$, and the speed up will be no more than $\frac{1}{s}$.

Again, suppose a machine with $N$ processors, the serial phase takes time $1$ and the parallel phase takes time $p$ if run on a single processor. Therefore:

• For the parallel phase, it takes $\frac{p}{N}$ on this machine.
• For the serial phase, it only runs on a single processor and it takes time $1$. Let $\alpha$ be the ratio of serial time to total execution time:

$$\alpha = \frac{1}{1+\frac{p}{N}} = \frac{N}{N+p}$$

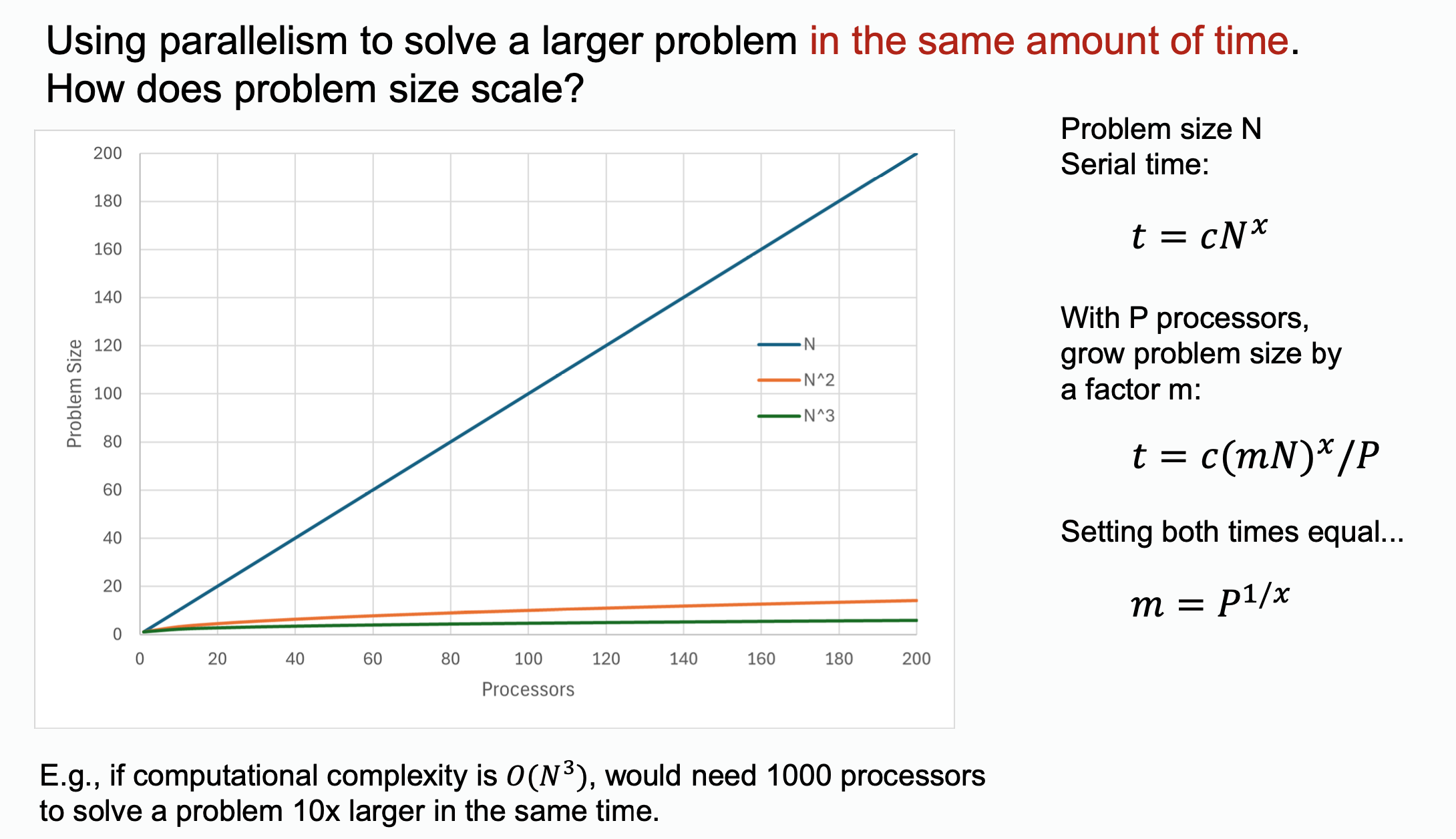
We can know that $\lim_{ n \to \infty } \alpha = 1$. The conclusion here is that if you have unlimited number of processors, the time consumption of a parallel program could be theoretically $0$.

warning

Adding cores(processors) causes overheads, as the processors need to communicate to switch information with each other, or they need to do some synchronization. Therefore, the actual calculation on speed up should consider the overhead term $o(P)$ caused by using $P$ processors. 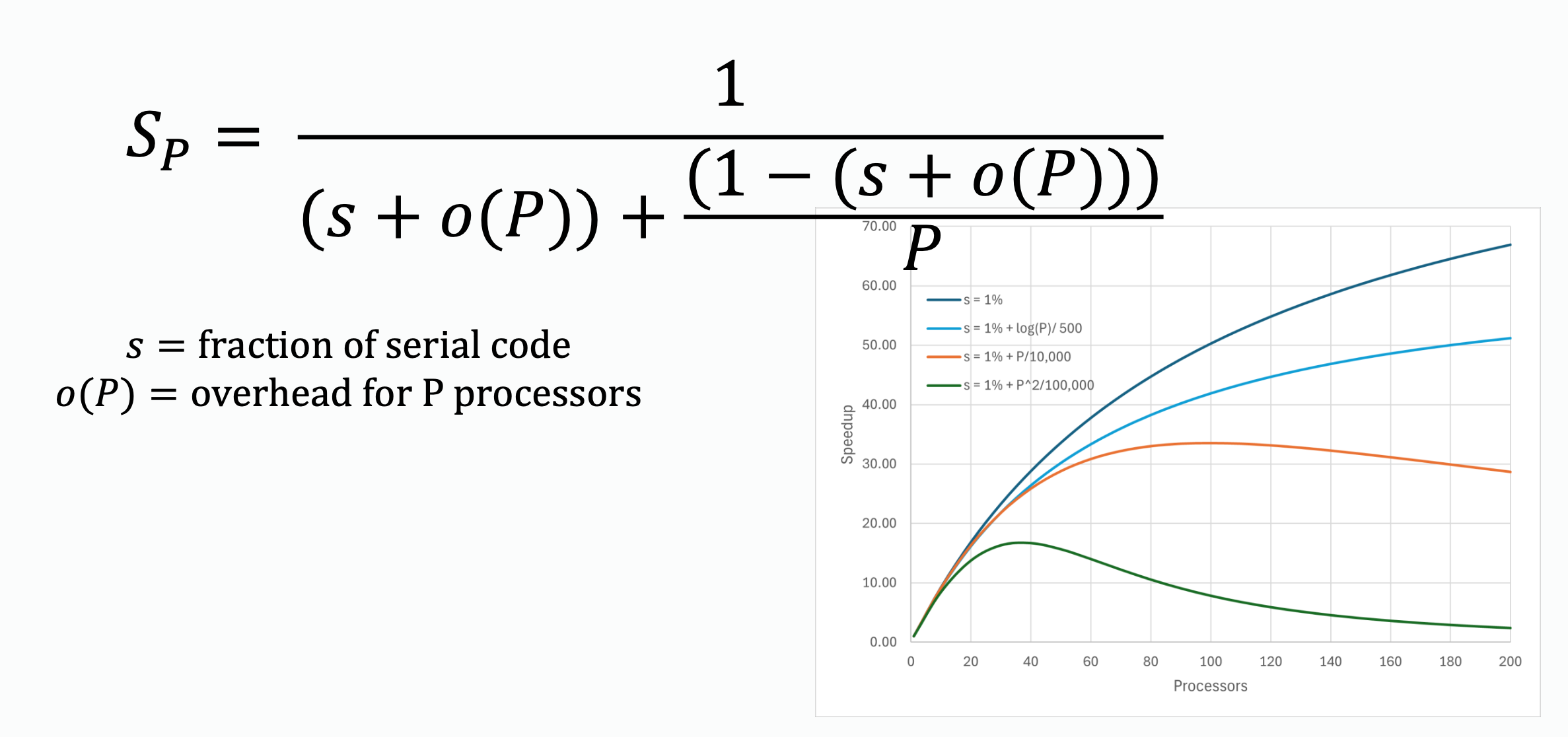The overhead term does not benefits from parallel execution, so it is considered as a constant. The overhead term sometimes becomes significant when it is growing with the growth of number of processors dramatically. Refer to the green line in the figure.

info

Definition Efficiency is defined as:

$$e = \frac{speedup}{number\ of\ processors}$$

However, considering efficiency $e$, $\lim_{ n \to \infty } e = 0$, which means that adding more processors brings the consequence of dropping efficiency, you are wasting processors and the efficiency is very lower. But the truth is, as $N$ increases, $p$ increase too, and the fraction of time $1-\alpha$ does not necessarily shrink with increasing $N$, and efficiency $e$ remains reasonable.

Gustafson's Law (scaled speedup)

Another law that measures speedup

note

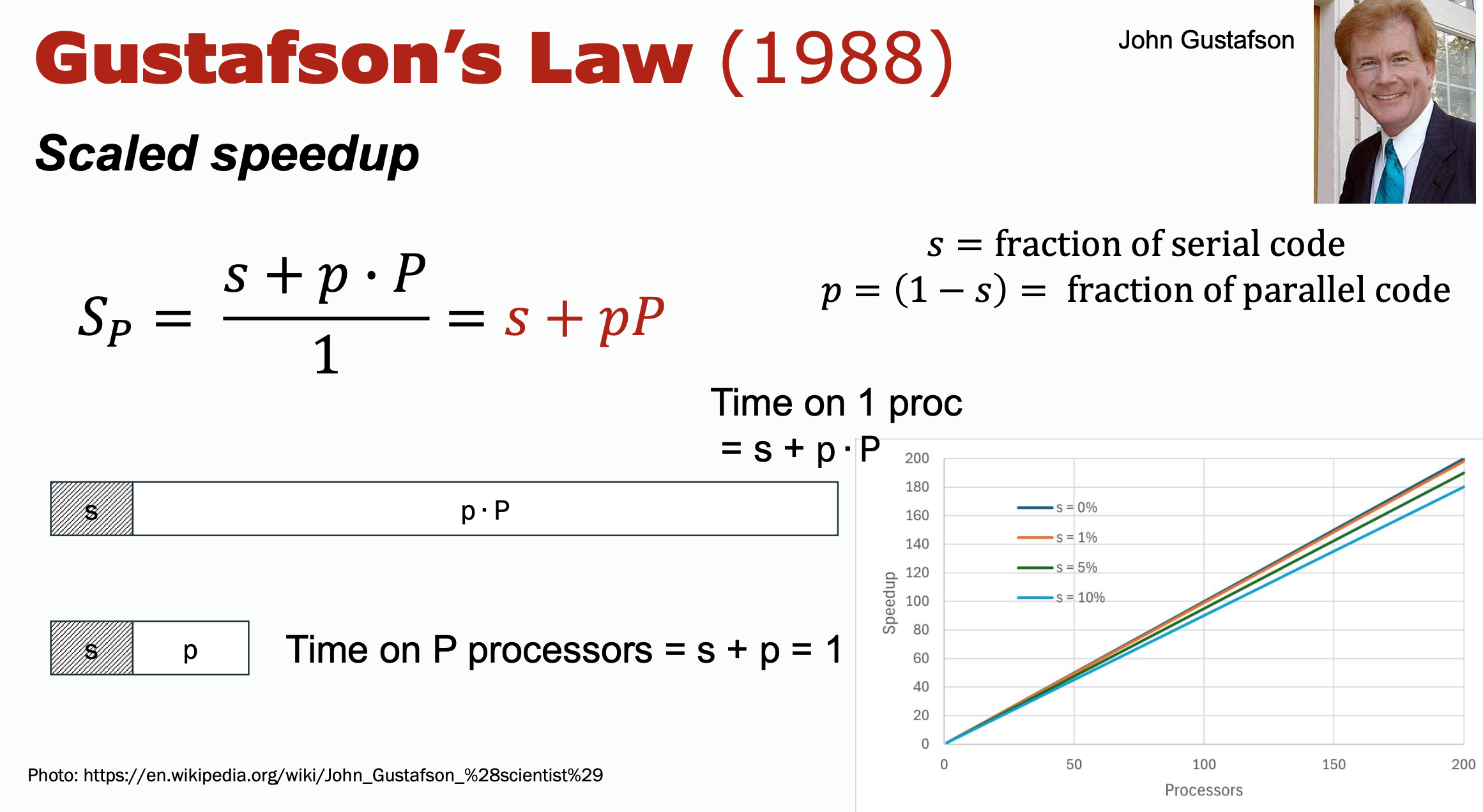
Amdahl’s Law is pessimistic, focusing on the inherent limitations due to the non-parallelizable portion of the workload. Gustafson’s Law is more optimistic, suggesting that increasing the problem size with more processors allows for greater speedup. Amdahl’s Law is more applicable when the problem size is fixed. Gustafson’s Law applies better when the problem size can scale with the number of processors.

How much bigger can the problem scale that it takes same time for a specific number of processors to solve the problem?